阅读记录：Landmark and Intensity-Based, Consistent Thin-Plate Spline Image Registration

DOI

10.1007/3-540-45729-1_33

Abstract

Landmark-based thin-plate spline image registration is one of the most commonly used methods for non-rigid medical image registration and anatomical shape analysis. It is well known that this method does not produce a unique correspondence between two images away from the landmark locations because interchanging the role of source and target landmarks does not produce forward and reverse transformations that are inverses of each other. In this paper, we present two new image registration algorithms that minimize the thin-plate spline bending energy and the inverse consistency error—the error between the forward and the inverse of the reverse transformation. The landmarkbased consistent thin-plate spline algorithm registers images given a set of corresponding landmarks while the intensity-based consistent thinplate spline algorithm uses both corresponding landmarks and image intensities. Results are presented that demonstrate that using landmark and intensity information to jointly estimate the forward and reverse transformations provides better correspondence than using landmarks or intensity alone.

基于地标的薄板样条插值图像配准是最常用的非刚性医学图像配准和解剖学形状分析方法之一。众所周知，这种方法不能在远离地标位置的两幅图像之间产生唯一的对应关系，因为互换源地标和目标地标的作用并不能产生互为逆变换的正向和反向变换。在本文中，我们提出了两种新的图像注册算法，它们能使薄板样条插值的弯曲能量和逆向一致性误差--正向和反向变换的逆向之间的误差最小。基于地标的一致薄板样条插值算法对给定的一组相应地标的图像进行配准，而基于强度的一致薄板样条插值算法则同时使用相应的地标和图像强度。结果表明，使用地标和强度信息来联合估计正向和反向变换，比单独使用地标或强度提供更好的对应关系。

Methods

Notation

Figure 1 shows two MRI images with corresponding landmarks that define the notation used throughout the paper. Assume that the template $T(y)$ and target** $S(x)$ images are defined on the continuous domain $\Omega = [0, 1)^2$ and were constructed from $N_1 × N_2$ pixel images using bilinear interpolation. Let $q_i \in \Omega$, and $p_i \in \Omega$, for $i = 1, . . . , M$, define corresponding landmarks in the template $T$ and target $S$ images, respectively. The forward transformation $h : \Omega \rightarrow \Omega$ is defined as the mapping that transforms $T$ into the shape of $S$ and the reverse transformation $g : \Omega \rightarrow \Omega$ is defined as the mapping that transforms $S$ into the shape of $T$ . The forward transformation $h(x) = x + u(x)$ defines the mapping from the coordinate system of the template to the target and the reverse transformation $g(y) = y + w(y)$ defines the mapping from the coordinate system of the target image to the template for $x, y \in \Omega^1$. The inverse of the forward transformation is defined as $h^{-1}(y) = y + \tilde{u}(y)$ and the reverse transformation is defined as $g^{-1}(x) = x + \tilde{w}(x)$.

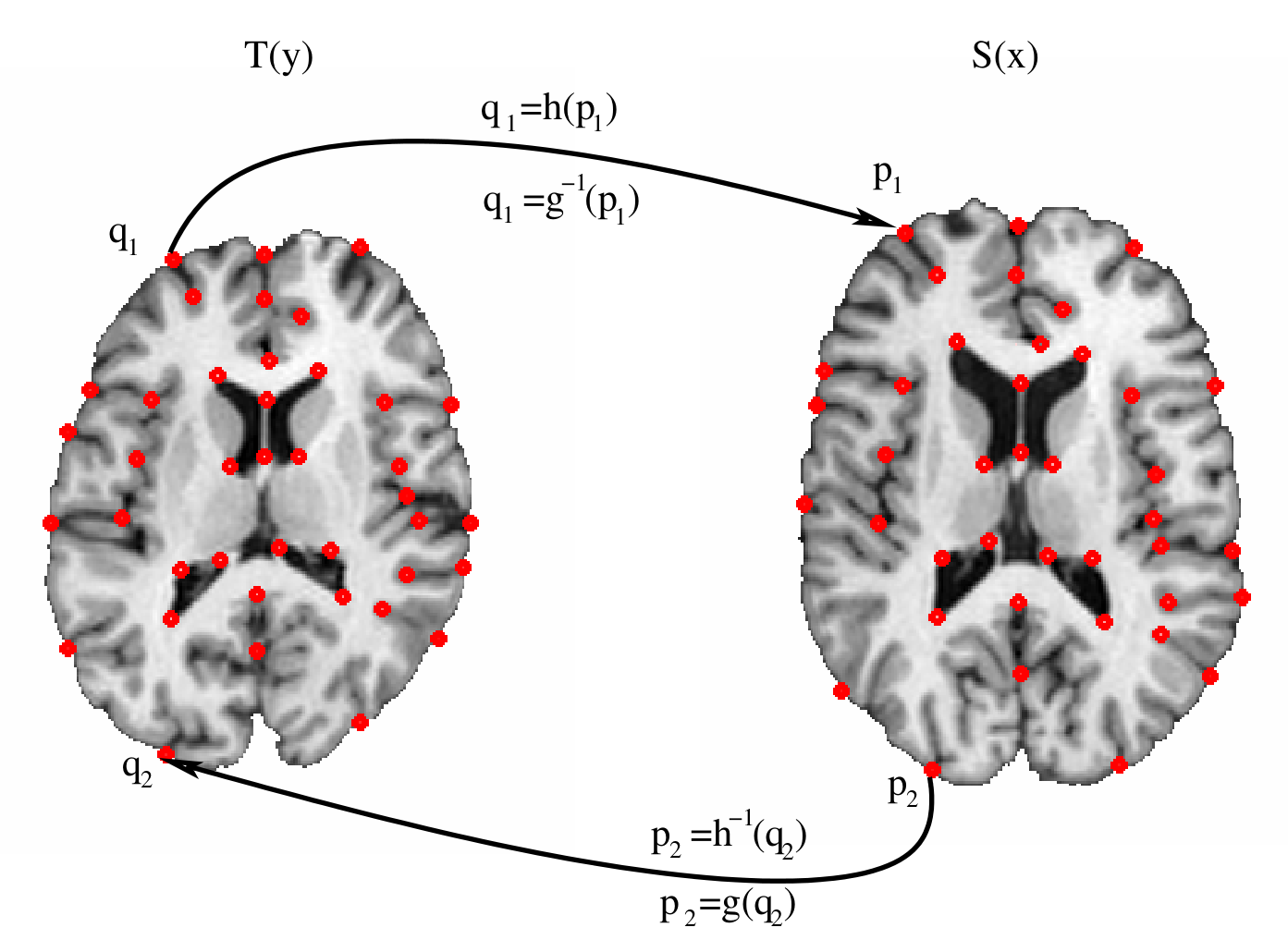
注解

标志点(landmark)正反变换能够一致，但是控制点为非标志点时，其 TPS 正向变换（红色）与逆向变换（绿色）会存在不一致性

$u(p_i)=q_i - p_i$

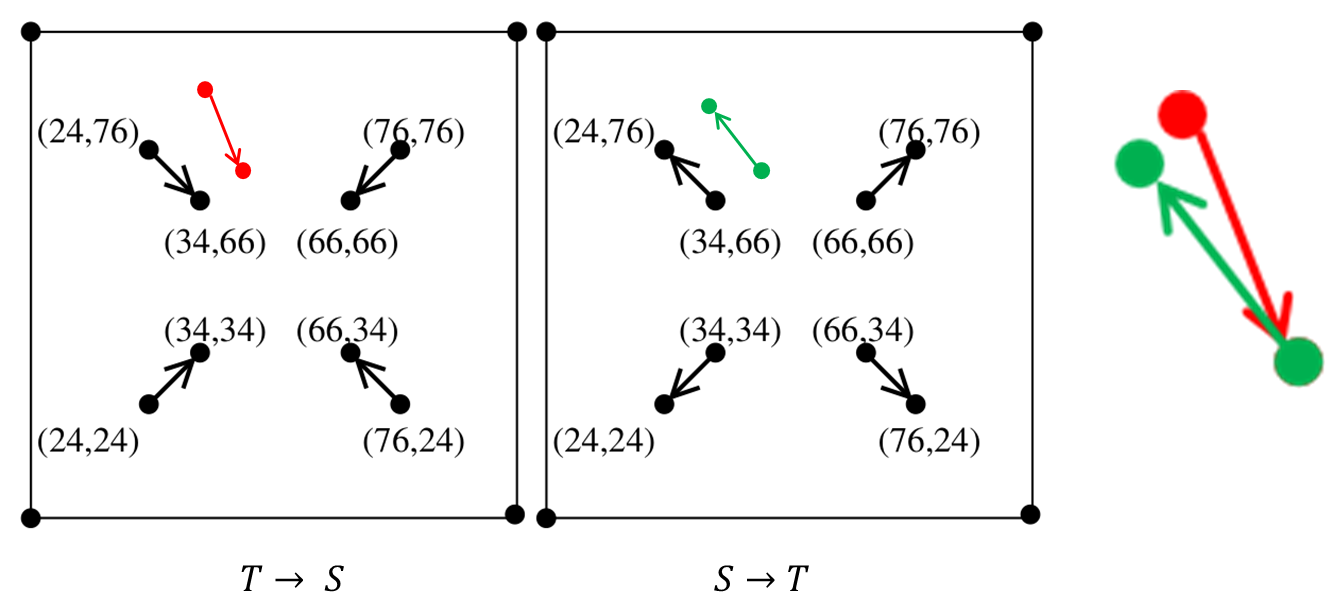
template $T$ target $S$

transformation		inverse（逆）
forward（正）	$T \rightarrow S$	$h(x) \rightarrow x$
	$h(x) = x + u(x)$ $x \rightarrow h(x) \approx y$	$h^{-1}(y) = y + \tilde{u}(y)$ $y \rightarrow h^{-1}(y) \approx x$
reverse（反）	$S \rightarrow T$	$g(y) \rightarrow y$
	$g(y) = y + w(y)$ $y \rightarrow g(y) \approx x$	$g^{-1}(x) = x + \tilde{w}(x)$ $x \rightarrow g^{-1}(x) \approx y$

Landmark-Based, Thin-Plate Spline Image Registration with Cyclic Boundary Conditions

$$C=\int_{\Omega}\|\mathcal{L} u(x)\|^{2}dx \tag{1}$$

$$C=\int_{\Omega}\left\|\nabla^{2} u(x)\right\|^{2} d x=\sum_{i=1}^{2} \int_{\Omega}\left(\frac{\partial^{2} u_{i}(x)}{\partial^{2} x_{1}}\right)^{2}+2\left(\frac{\partial^{2} u_{i}(x)}{\partial x_{1} \partial x_{2}}\right)+\left(\frac{\partial^{2} u_{i}(x)}{\partial^{2} x_{2}}\right)^{2} d x_{1} d x_{2} \tag{2}$$

where $u(p_i)=q_i - p_i$ for $i = 1, . . . , M$

It is well known that the TPS displacement field $u(x)$ that minimizes the bending energy defined by $Eq. 2$ has the form

$$u(x)=\sum_{i=1}^{M} \xi_{i} \phi\left(x-p_{i}\right)+A x+b \tag{3}$$

where $φ(r) = r^2 log r$ and $\xi_{i}$ are $2 × 1$ weighting vectors. The $2 × 2$ matrix $A = [a1, a2]$ and the $2 × 1$ vector $b$ define the affine transformation where $a_1$ and $a_2$ are $2 × 1$ vectors.
The unknown parameters $W = [\xi_{1}, . . . , \xi_{M}, a_1, a_2, b]^T$ are determined by substituting the landmark constrains into $Eq. 3$ and solving the resulting equations. Let $\phi_{i,j} = \phi(|p_i - q_j|)$ build the matrix

$$K=\left[\begin{array}{cc} \Phi & \Lambda \\ \Lambda^{T} & O \end{array}\right] \text { where } \Phi=\left[\begin{array}{cccc} \phi_{1,1} & \phi_{1,2} & \ldots & \phi_{1, M} \\ \phi_{2,1} & \phi_{2,2} & \ldots & \phi_{2, M} \\ \vdots & \vdots & \ddots & \vdots \\ \phi_{M, 1} & \phi_{M, 2} & \ldots & \phi_{M, M} \end{array}\right], \quad \Lambda=\left[\begin{array}{ccc} p_{1,1} & p_{1,2} & 1 \\ p_{2,1} & p_{2,2} & 1 \\ \vdots & \vdots & \vdots \\ p_{M, 1} & p_{M, 2} & 1 \end{array}\right] \tag{4}$$

and $O$ is a $3×3$ matrix of zeros. Also, define the $(M +3)×2$ matrix of landmark displacements as $D = [d_1, . . . , d_M, 0, 0, 0]^T$ where $d_i = q_i - p_i$ for $i = 1, . . . , M$. The equations formed by substituting the landmark constrains into $Eq. 3$ can be written in matrix form as $D = KW$. The solution $W$ to this matrix equation is determined by least squares estimation since the matrix $K$ is not guaranteed to be full rank.

注解

矩阵 $W$ 应该由最小二乘法求解，因为$K$不一定满秩，即不一定可逆（方阵：矩阵满秩等价于矩阵可逆，非方阵是广义逆）。由$Ax=b$的最小二乘法求解为$x = (A^TA)^{-1}A^Tb$，则上述$W = (K^TK)^{-1}K^TD$.

Landmark Consistent Thin-Plate Spline Registration

PDF